Formularium - Statistiek deel 2

1-2 Steekproevenverdeling

• concepten (herhaling statistiek 1)
  • populatie
  • (populatieverdeling)
  • (populatie)parameter $\vartheta$
  • toevalsvariabele (TV)
    • heeft een verdeling, gemiddelde, variantie, ...
    • symbolen altijd in hoofdletters ($X, \overline X, S_X, \ldots$)
      • uitzondering: $r_{XY}$
  • trekking op zuiver toevallig wijze (ZTW)
    • met teruglegging
  • steekproef
    • steekproefgrootte $n$
  • statistische maat
    • vast recept
    • input: een steekproef
    • output: exact één getal
    • symbolen altijd met kleine letters
    • voorbeelden
      • $\overline x$
      • $s_x$
  • statistiek $T$
    • gelijkaardig aan statistische maat
    • input: meerdere steekproeven van gelijke grootte $n$
    • output: toevalsvariabele
      • dus niet meer één getal
      • dus symbolen met hoofdletters
    • voorbeelden
      • $\overline X_n$
      • $S_{X_n}$
  • standaardfout / standard error (SE)
    • standaardafwijking $\sigma_T$ van statistiek $T$
  • steekproevenverdeling $\pi_T$ of $\varphi_T$
    • verdelingsfunctie van statistiek $T$
  • (parameter)schatter $\hat\vartheta$
    • statistiek die populatieparameter $\vartheta$ benadert
    • voorbeelden
      • $\overline X$ voor $\mu$
      • $S'_X$ voor $\sigma_X$
  • i.d. = identically distributed
  • i.i.d. = independent and identically distributed
    • onafhankelijk
      • $P(X_2 \mid X_1) = P(X_2)$
      • $P(X_1 \cap X_2) = P(X_1) \cdot P(X_2)$
    • identiek verdeeld
      • $\pi_{X_1}(x) = \pi_{X_2}(x)$ of
      • $\varphi_{X_1}(x) = \varphi_{X_2}(x)$
      • niet: $X_1 = X_2$
• enumeratieve methode van steekproevenverdeling
  • bepaal verdeling door alle combinaties uit te schrijven
  • enkel haalbaar voor kleine $n$

Twee studenten kiezen elk random één van de getallen 0, 1 of 2. Wat is de kans dat het gemiddelde van hun getallen kleiner is dan 1.5?

$$P(\overline X < 1.5) = \frac{6}{3^2} \approx 0.6667$$

$X_1$	$X_2$	$\overline X_2$
0	0	0.0
0	1	0.5
0	2	1.0
1	0	0.5
1	1	1.0
1	2	1.5
2	0	1.0
2	1	1.5
2	2	2.0

1.1 Gemiddelde en variantie van $\overline X$

• met teruglegging: $X_1, \ldots, X_n$ i.i.d.
  • $\mu_{\overline X} = \mu_X$
  • $\sigma_{\overline X}^2 = \dfrac{\sigma_X^2}{n}$ en $\sigma_{\overline X} = \dfrac{\sigma_X}{\sqrt n}$
    • dus schatting van populatiegemiddelde wordt beter en beter (kleinere spreiding) als $n$ groter wordt
• zonder teruglegging: $X_1, \ldots, X_n$ i.d.
  • $\mu_{\overline X} = \mu_X$
  • eindige populatie
    • populatiecorrectiefactor (PCF): $\dfrac{N-n}{N-1}$
    • $\sigma_{\overline X}^2 = \dfrac{\sigma_X^2}{n} \cdot \dfrac{N-n}{N-1}$
  • oneindige populatie
    • zelfde als met teruglegging
    • $\displaystyle \sigma_{\overline X}^2 = \lim_{N \to \infty} \dfrac{\sigma_X^2}{n} \cdot \dfrac{N-n}{N-1} = \dfrac{\sigma_X^2}{n}$
    • gebruik als benadering vanaf $N \geq 20n$

We trekken met teruglegging een steekproef van grootte 70 uit een eindige populatie van grootte 500 met populatiegemiddelde 220 en variantie 324. Wat is de standaarddeviatie van het steekproefgemiddelde?

• gegeven
  • $N = 500$
  • $n = 70$
  • met teruglegging
  • $\mu_X = 220$
  • $\sigma_X^2 = 324$
• gevraagd
  • $\sigma_{\overline X}$
• oplossing
  • $N < 20n = 1400$
    • dus correctiefactor voor teruglegging nodig
  • $\sigma_{\overline X}^2$
    • $= \dfrac{\sigma_X^2}{n} \cdot \dfrac{N-n}{N-1}$
    • $= \dfrac{324}{70} \cdot \dfrac{500-70}{500-1}$
    • $= \dfrac{324}{70} \cdot \dfrac{430}{499}$
    • $\approx 3.9885$
  • $\sigma_{\overline X}$
    • $= \sqrt{\sigma_{\overline X}^2}$
    • $\approx 1.9971$
• antwoordmogelijkheden
  • A: $\sigma_{\overline X}$ met correctiefactor
  • B: $\sigma_{\overline X}^2$ met correctiefactor
  • C: $\sigma_{\overline X}$ zonder correctiefactor
  • D: $\sigma_{\overline X}^2$ zonder correctiefactor

2.1 Verdeling van $\overline X$

• als $X \sim N(\mu_X, \sigma^2_X)$
  • dan $\overline X \sim N\left(\mu_X, \dfrac{\sigma^2_X}{n}\right)$
• als $X$ niet normaal verdeeld is
  • als $n > 30$
    • met teruglegging: $X_1, \ldots, X_n$ i.i.d.
      • centrale limietstelling: $\overline X \sim N\left(\mu_X, \dfrac{\sigma^2_X}{n}\right)$
    • zonder teruglegging
      • eindige populatie
        • $\overline X \sim N\left(\mu_X, \dfrac{\sigma^2_X}{n} \cdot \dfrac{N-n}{N-1}\right)$
      • oneindige populatie of $N \geq 20n$
        • centrale limietstelling: $\overline X \sim N\left(\mu_X, \dfrac{\sigma^2_X}{n}\right)$
  • als $n \leq 30$
    • andere oplossing (computersimulatie, ...)

Een psychologisch onderzoeker bestudeert reactietijden bij een cognitieve taak. De reactietijden zijn normaal verdeeld met verwachte waarde $\mu_X = 600$ milliseconden en een standaardafwijking $\sigma_X = 100$ milliseconden. Als de onderzoeker een steekproef van 25 personen neemt, wat is dan de kans dat de gemiddelde reactietijd van deze 25 personen meer is dan 620 milliseconden?

• gegeven
  • $X \sim N(600, 100^2)$
    • dus oneindige populatie
  • $n= 25$
• gevraagd
  • $P(\overline X_{25} > 620)$
• oplossing
  • $\sigma_{\overline X} = \frac{100}{\sqrt{25}} = 20$
  • $\overline X \sim N(600, 20^2)$
  • $P(\overline X_{25} > 620)$
  • $= 1 - P(\overline X_{25} \leq 620)$
  • $= 1 - P(\frac{\overline X_{25} - 600}{20} \leq \frac{620-600}{20})$
  • $= 1 - P(Z_{\overline X_{25}} \leq \frac{620-600}{20})$
  • $= 1 - \Phi_{Z_{\overline X_{25}}}^{-1}(1)$
  • $\in [0.155, 0.160]$

De tijd die een patiënt doorbrengt bij de psycholoog heeft een exponentiële verdeling. De verwachte duur van een therapiesessie is 1 uur en de standaardafwijking is 1 uur. Een psycholoog heeft 70 patiënten in behandeling. Wat is de kans dat de gemiddelde therapiesessie langer duurt dan 50 minuten?

• gegeven
  • $X$: tijd bij psycholoog (in minuten)
  • $\mu_X = 60$
  • $\sigma_X = 60$
  • $X \sim Expon(\frac{1}{\mu_X})$
  • $n = 70$
• gevraagd
  • $P(\overline X > 50)$
• oplossing
  • $X$ niet normaal verdeeld
  • $n > 30$
  • oneindige populatie
  • centrale limietstelling: $\overline X \sim N\left(60, \dfrac{60^2}{70}\right)$
  • $\sigma_{\overline X} \approx 7.1714$
  • $P(\overline X > 50)$
  • $= 1 - P(\overline X \leq 50)$
  • $= 1 - P(\frac{\overline X - 60}{7.1714} \leq \frac{50 - 60}{7.1714})$
  • $= 1 - \Phi_Z^{-1}(-1.3944)$
  • $\in [0.915, 0.920]$

Een farmabedrijf telt 3500 werknemers. Uit voorgaande tests is gebleken dat de gemiddelde IQ-score van de werknemers 110 is met een standaardafwijking gelijk aan 12. Je neemt een steekproef van 200 verschillende werknemers en je vraagt je af of hun IQ-scores representatief zijn voor de gehele werkvloer. Wat is de kans dat het gemiddeld IQ in je steekproef binnen 2 punten van het gemiddelde van het ganse bedrijf valt?

• gegeven
  • $X$: IQ van werknemers farmabedrijf
  • $N = 3500$
  • $\mu_X = 110$
  • $\sigma_X = 12$
  • $n = 200$
• gevraagd
  • $P(|\overline X - \mu_X| < 2)$
  • $= P(108 \leq \overline X \leq 112)$
  • $= P(\overline X \leq 112) - P(\overline X < 108)$
• oplossing
  • $X$ niet normaal verdeeld
    • (IQ is meestal wel normaal verdeeld, maar hier niet gegeven)
  • $n > 30$
  • zonder teruglegging
  • eindige populatie met $N < 20n$
    • dus correctiefactor nodig
  • $\overline X \sim N\left(\mu_X, \dfrac{\sigma^2_X}{n} \cdot \dfrac{N-n}{N-1}\right)$
  • $\sigma_{\overline X} \approx \sqrt{0.6791} \approx 0.8240$
  • $P(\overline X \leq 112) - P(\overline X < 108)$
  • $= \Phi_Z^{-1}(\frac{112-110}{0.8240}) - \Phi_Z^{-1}(\frac{108-110}{0.8240})$
  • $= \Phi_Z^{-1}(2.4271) - \Phi_Z^{-1}(-2.4271)$
  • $\in [0.984, 0.986]$

2.2 Toepassing: normale benadering voor binomiale verdeling

• $X_i \sim Bern(\vartheta)$
  • $\mu_{X_i} = \vartheta$
  • $\sigma_{X_i}^2 = \vartheta(1 - \vartheta)$
• $Y = \sum_{i=1}^n X_i \sim Bin(n, \vartheta)$
  • $\mu_Y = n\vartheta$
  • $\sigma_Y^2 = n\vartheta(1 - \vartheta)$
• exacte oplossing vraagt vaak veel rekenwerk
• alternatief: benadering via normale verdeling
• merk op: $\overline X_n = \frac{1}{n} \sum_{i=1}^n X_i = \frac{Y}{n}$
  • $\mu_{\overline X_n} = \vartheta$
  • $\sigma_{\overline X_n}^2 = \frac{\vartheta(1 - \vartheta)}{n}$
• als $n\vartheta \geq 10$ en $n(1 - \vartheta) \geq 10$
  • met teruglegging: $X_1, \ldots, X_n$ i.i.d.
    • centrale limietstelling
      • $\overline X_n \sim N\left(\vartheta, \frac{\vartheta(1 - \vartheta)}{n}\right)$
      • $Y \sim N(n\vartheta, n\vartheta(1 - \vartheta))$
  • zonder teruglegging
    • eindige populatie ($N < 20n$)
      • benadering niet geldig
    • oneindige populatie of $N \geq 20n$
      • idem als met teruglegging
• continuiteitscorrectie

Bionomiaal	Normaal
$P(X = c)$	$P(c-0.5 < X < c+0.5)$
$P(X > c)$	$P(X > c + 0.5)$
$P(X \geq c)$	$P(X > c - 0.5)$
$P(X < c)$	$P(X < c - 0.5)$
$P(X \leq c)$	$P(X < c + 0.5)$

6 procent van de bevolking is universele bloeddonor (kan bloed doneren aan iedereen). Een ziekenhuis heeft 10 universele bloeddonoren nodig. Er bieden zich 200 kandidaten aan om bloed te geven. Wat is de kans dat hier minstens 10 universele bloeddonoren bij zijn?

• gegeven
  • $Y$: aantal universele bloeddonoren
  • $\vartheta = 0.06$
  • $n = 200$
• gevraagd
  • $P(Y \geq 10)$
• oplossing
  • $n\vartheta = 12 \geq 10$ en $n(1 - \vartheta) = 188 \geq 10$
  • oneindige populatie
  • $Y \sim N(n\vartheta, n\vartheta(1 - \vartheta)) \sim N(12, 11.28)$
  • continuiteitscorrectie
    • $P(Y \geq 10) \to P(Y > 9.5)$
  • $P(\frac{Y - 12}{\sqrt{11.28}} > \frac{9.5 - 12}{\sqrt{11.28}})$
  • $= 1- P(\frac{Y - 12}{\sqrt{11.28}} \leq \frac{9.5 - 12}{\sqrt{11.28}})$
  • $= 1 - \Phi_Z^{-1}(-0.7444)$
  • $\in [0.770, 0.775]$

2.3 Andere steekproevenverdelingen

• als $X \sim N(\mu_X, \sigma_X^2)$
  • dan $\dfrac{(n-1)S_X^{\prime 2}}{\sigma_X^2} \sim \chi^2_{df=n-1}$
  • en dus $\dfrac{nS_X^2}{\sigma_X^2} \sim \chi^2_{df=n-1}$
• rest: zie formularium

Een socioloog onderzoekt de onderlinge verschillen in het aantal uren per week dat studenten aan een universiteit gemiddeld besteden aan sociale media. Eerder onderzoek heeft aangetoond dat de populatiestandaarddeviatie van het aantal uren dat studenten op sociale media doorbrengen 4 uur is. Voor een steekproef van 35 studenten blijkt de steekproefvariantie $S_X^{\prime 2}$ in hun gebruik van sociale media 20 uur te zijn. Hoe extreem is deze waarde, m.a.w. wat is de kans om een steekproefvariantie te observeren die minstens even groot is? (bij een even grote steekproef)

• gegeven
  • $X$: uren sociale media
  • $\sigma_X = 4$
  • $n = 35$
  • $S_X^{\prime 2} = 20$
• gevraagd
  • $P(S_X^{\prime 2} \geq 20)$
• oplossing
  • extra assumptie: $X$ normaal verdeeld
  • $\dfrac{34S_X^{\prime 2}}{4^2} \sim \chi^2_{df=34}$
  • $P(S_X^{\prime 2} \geq 20)$
  • $= P(\frac{34 S_X^{\prime 2}}{16} \geq \frac{34 \cdot 20}{16})$
  • $= 1 - P(\frac{34 S_X^{\prime 2}}{16} < \frac{34 \cdot 20}{16})$
  • $= 1 - P(\frac{34 S_X^{\prime 2}}{16} \leq 42.5)$
  • $= 1 - \Phi_{\chi^2}^{-1}(42.5)$
  • $\in [0.15, 0.20]$

3 Schatters

• kwaliteit
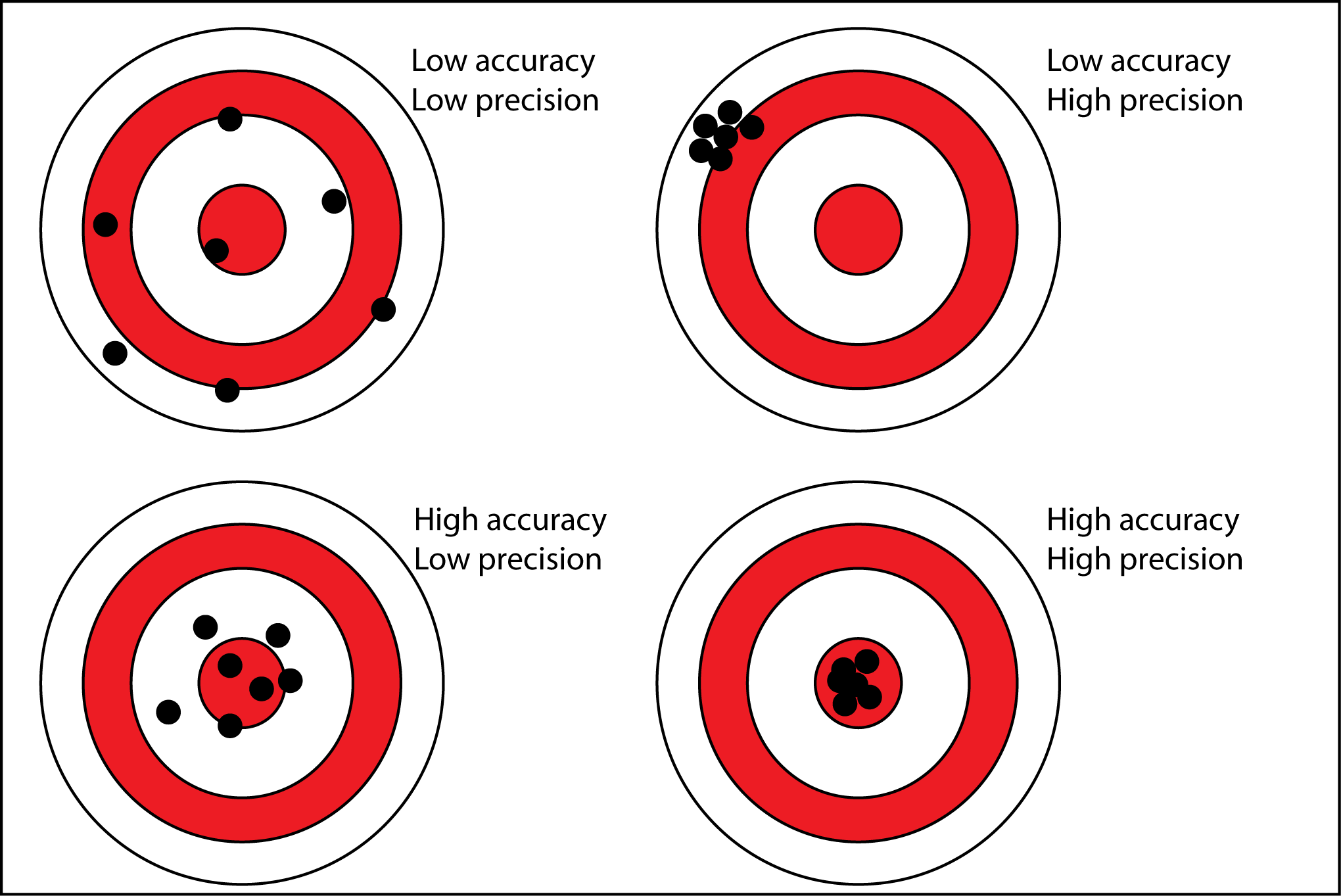
  • vertekening = bias
    • $E[\hat\vartheta_n] - \vartheta$
  • zuiver
    • $E[\hat\vartheta_n] - \vartheta = 0 \iff E[\hat\vartheta_n] = \vartheta$
  • asymptotisch zuiver
    • $\displaystyle \lim_{n \to \infty} E[\hat\vartheta_n] = \vartheta$
  • variabiliteit
    • $\sigma_{\hat\vartheta_n}^2$
  • nauwkeurigheid / betrouwbaarheid
    • kleine variabiliteit
  • mean squared error (MSE)
    • $E[(\hat\vartheta_n - \vartheta)^2] = \sigma_{\hat\vartheta_n}^2 + (E[\hat\vartheta_n] - \vartheta)^2$
  • consistente schatter
    • $\displaystyle \lim_{n \to \infty} MSE = 0$
    • dus als $\displaystyle \lim_{n \to \infty} \sigma_{\hat\vartheta_n}^2 = 0$ EN asymptotisch zuiver

3.1 Puntschatter voor het gemiddelde

• schatter $\overline X_n$ voor $\mu_X$
• eigenschappen
  • zuiver
  • asymptotisch zuiver
  • consistent

Veronderstel dat $X_1, X_2, X_3$ i.i.d. toevalsvariabelen zijn met verwachte waarde $\mu_X$. Welk van onderstaande schatters voor $\mu_X$ is zuiver? Welke schatter zou je verkiezen? En waarom?

1. $\frac{1}{3}(X_1 + X_2 + X_3)$
2. $\frac{1}{2}(X_1 + X_2)$
3. $0.75X_1 + 0.75X_2 - 0.5X_3$
4. $\frac{1}{2}(X_1 + X_2 + X_3)$

• zuiver
  • (1) ja
  • (2) ja: $E[\frac{1}{2}(X_1 + X_2)] = \frac{1}{2}(E[X_1] + E[X_2]) = \frac{1}{2}(\mu_X + \mu_X) = \mu_X$
  • (3) ja
  • (4) nee
• beste keuze
  • (1) dit is $\overline X$
    • neemt elke toevalsvariabele mee in rekening
    • geeft elke variabele evenveel gewicht

3.2 95% intervalschatting voor het gemiddelde

• assumpties
  • $X \sim N(\mu_X, \sigma_X^2)$
  • gekende variantie
• bereken betrouwbaarheidsinterval (BI)
  • ondergrens OG
  • bovengrens BG
• $\alpha = 1 - 95\% = 0.05$
• interval waarbinnen $\mu_X$ zich in 95% van alle steekproeven bevindt
  • in symbolen: $P(OG \leq \mu_X \leq BG) = 0.95$
• verschillend per steekproef
• symmetrisch rond $\overline x$
  • merk op: BIs zijn niet voor alle parameters symmetrisch (maar wel voor gemiddelde)
• kritieke waarden
  • $-1.96 = \Phi_Z^{-1}(\frac{\alpha}{2}) = z_{0.025}^*$
  • $+1.96 = \Phi_Z^{-1}(1 - \frac{\alpha}{2}) = z_{0.975}^*$
• $\overline x \pm 1.96 \dfrac{\sigma_X}{\sqrt n}$
• foutenmarge $m = 1.96 \dfrac{\sigma_X}{\sqrt n} = \dfrac{bg - og}{2}$

Gegeven een normaalverdeelde toevalsvariabele 𝑋 met gekende populatievariantie. Waaraan is het 95% BI voor $\mu_X$ gelijk als je gebruikmaakt van onderstaande gegevens?

• $\overline x = 8.5$
• $\sigma_X = 2$
• $n = 30$

• gegeven
  • $\overline x = 8.5$
  • $\sigma_X = 2$
  • $n = 30$
  • $X \sim N(\ldots, 2^2)$
• gevraagd
  • 95% BI voor $\mu_X$
• oplossing
  • $\overline x \pm 1.96 \dfrac{\sigma_X}{\sqrt n}$
  • $= 8.5 \pm 1.96 \dfrac{2}{\sqrt{30}}$
  • $= 8.5 \pm 0.7157$
  • $= [7.7843, 9.2157]$

3.3 C-intervalschatting voor het gemiddelde

• assumpties
  • $X \sim N(\ldots, \sigma_X^2)$
    • anders: zie vorig hoofdstuk over bepaling verdeling $\overline X$
  • gekende variantie $\sigma_X^2$
• gelijkaardig aan hierboven, behalve ...
• $\alpha = 1 - C$
• kritieke waarden
  • $\Phi_Z^{-1}(\frac{\alpha}{2}) = z_{\frac{\alpha}{2}}^*$
  • $\Phi_Z^{-1}(1 - \frac{\alpha}{2}) = z_{1-\frac{\alpha}{2}}^*$
• $\overline x \pm z_{1-\frac{\alpha}{2}}^* \dfrac{\sigma_X}{\sqrt n}$
• foutenmarge $m = z_{1-\frac{\alpha}{2}}^* \dfrac{\sigma_X}{\sqrt n} = \dfrac{bg - og}{2}$
• hogere $C$
  • lagere $\alpha$
  • grotere foutenmarge
  • breder interval
  • meer zekerheid
  • minder nauwkeurig
• lagere $C$
  • hogere $\alpha$
  • lagere foutenmarge
  • smaller interval
  • minder zekerheid
  • meer nauwkeurig

Gegeven een normaal verdeelde toevalsvariabele met gekende populatievariantie. Waaraan is het 99% BI voor $\mu_X$ gelijk als je gebruikmaakt van onderstaande gegevens?

• $\overline x = 8.5$
• $\sigma_X = 3$
• $n = 25$

• gegeven
  • $\overline x = 8.5$
  • $\sigma_X = 3$
  • $n = 25$
  • $X \sim N(\ldots, 3^2)$
• gevraagd
  • 99% BI voor $\mu_X$
• oplossing
  • $\alpha = 1 - 0.99 = 0.01$
  • $z_{1-\frac{\alpha}{2}}^* = z_{0.995}^* = 2.5758$
  • $\overline x \pm 2.5758 \dfrac{\sigma_X}{\sqrt n}$
  • $= 8.5 \pm 2.5758 \dfrac{3}{\sqrt{25}}$
  • $= 8.5 \pm 1.5455$
  • $= [6.9545, 10.0455]$

Het 99% betrouwbaarheidsinterval zal in vorige oefening ... zijn aan/dan het 90% betrouwbaarheidsinterval

• breder

3.4 C-intervalschatting voor andere parameters

• zie formularium

Gegeven een normaal verdeelde variabele met onbekende variantie. Als je gebruikmaakt van onderstaande gegevens, hoeveel bedraagt dan een 80% BI voor $\sigma_X^2$?

• $s_x^2 = 3$
• $n = 30$

• gegeven
  • $X \sim N(?, ?)$
  • $s_x^2 = 3$
  • $n = 30$
• gevraagd
  • 80% BI voor $\sigma_X^2$
• oplossing
  • $\dfrac{nS_X^2}{\sigma_X^2} \sim \chi^2_{df=n-1}$
  • $P\left(\Phi_{\chi^2}^{-1}(0.10) \leq \dfrac{nS_X^2}{\sigma_X^2} \leq \Phi_{\chi^2}^{-1}(0.90)\right) = 0.80$
  • $\iff P\left(19.7677 \leq \dfrac{90}{\sigma_X^2} \leq 39.0875\right) = 0.80$
  • $\iff P(2.3025 \leq \sigma_X^2 \leq 4.5529) = 0.80$

4 Hypothesetoetsing

• nulhypothes $H_0$
• alternatieve hypothese $H_1$
  • eenzijdig ($<, \leq, \geq, >$)
  • tweezijdig ($\neq$)
• soorten toetsen
  • Z-toets (dit hoofdstuk)
    • parameter: $\mu_X$
    • $\sigma_X^2$ bekend
    • drie manieren
      • via kritieke waarden
      • via p-waarde
      • via BI
  • t-toets (zie hoorcollege 6)
    • parameter: $\mu_X$
    • $\sigma_X^2$ onbekend
  • andere grootheden (zie hoorcollege 7)
  • $\chi^2$ toets voor goodness of fit (zie hoorcollege 10)

Na het tweede zitexamen berekent een docent de verschilscores tussen de behaalde score in januari (J) en de behaalde score in september (S). Hij wil nagaan of studenten in september gemiddeld hoger scoren dan in januari. Formuleer de achterliggende $H_1$.

• $H_0: \mu_{S-J} = 0$
• $H_1: \mu_{S-J} > 0$

4.1 Tweezijdige toetsen via kritieke waarden

• stap 1: bepaal $H_0$ en $H_1$
• stap 2: bepaal $n$ en significantieniveau $\alpha$
  • $\alpha$ groter: sneller $H_0$ verwerpen
  • $\alpha$ kleiner: sneller $H_0$ aanvaarden
• stap 3: kies geschikte toetsstatistiek (TS) en bijhorende steekproevenverdeling onder $H_0$
• stap 4: bereken toetsstatistiekwaarde (ts) onder $H_0$
• stap 5: welke ts waarden zijn verdacht (doen vermoeden dat $H_1$ waar is)?
• stap 6: bereken kritieke waarden
  • bepalen aanvaardings- en verwerpingsgebied
  • tweezijdige $H_1$: $z_{\frac{\alpha}{2}}^*$ en $z_{1 - \frac{\alpha}{2}}^*$
  • beslissing
    • $ts$ in aanvaardingsgebied: aanvaard $H_0$ op significantieniveau $\alpha$
    • $ts$ in verwerpingsgebied: verwerp $H_0$ op significantieniveau $\alpha$
      • synoniem: kritiek gebied

Een onderzoeker beschikt over normaalverdeelde gegevens en wil de volgende hypothese toetsen met $\alpha = 0.01$ en $\sigma_X = 16$: $H_0: \mu_X = 50$ vs. $H_1: \mu_X \neq 50$. Om de hypothese te toetsen trekt de onderzoeker een steekproef van 64 personen; het steekproefgemiddelde in deze steekproef bedraagt 44. Welke beslissing neem je? Voer de hypothesetoets uit m.b.v. kritieke waarden.

• gegeven
  • $\alpha = 0.01$
  • $\sigma_X = 16$
  • $n = 64$
  • $\overline x = 44$
• gevraagd
  • hypothesetoetsing m.b.v. kritieke waarden
• oplossing
  • stap 1
    • $H_0: \mu_X = 50$
    • $H_1: \mu_X \neq 50$ (tweezijdig)
  • stap 2
    • $n = 64$
    • $\alpha = 0.01$
  • stap 3
    • $TS = \dfrac{\overline X - \mu_X}{\frac{\sigma_X}{\sqrt n}} \sim N(0, 1)$
  • stap 4
    • $ts = \dfrac{44 - 50}{16 / \sqrt{64}} = -3$
  • stap 5
    • $ts$ sterk verschillend van nul is verdacht, dus beide staarten
  • stap 6
    • $z_{\frac{\alpha}{2}}^* = -2.5758$
    • $z_{1 - \frac{\alpha}{2}}^* = 2.5758$
    • $ts = -3$ valt buiten dit bereik (in verwerpingsgebied)
    • dus verwerp $H_0$ op significantieniveau $0.01$

4.2 Tweezijdige toetsen via p-waarde

• stap 1-5: idem
• stap 6
  • p-waarde = overschrijdingskans: kans om - onder $H_0$ - een minstens even verdachte $ts$ waarde te observeren
    • tweezijdige $H_1$: tweemaal de kans op de kleinste staart
    • kleinste staart links: $p = 2P(TS \leq ts)$
    • kleinste staart rechts: $p = 2P(TS \geq ts)$
    • bij symmetrische verdelingen: $p = 2P(TS \leq - |ts|)$
  • beslissing
    • als $p \leq \alpha$
      • behoorlijk verdacht om een waarde als $ts$ tegen te komen als $H_0$ waar is
      • maar onze steekproef leverde wel die $ts$ op
      • dus initiele assumptie ($H_0$) is waarschijnlijk fout
      • verwerp $H_0$ op significantieniveau $\alpha$
    • als $p > \alpha$
      • niet erg verdacht om een waarde als $ts$ tegen te komen als $H_0$ waar is
      • aanvaard $H_0$ op significantieniveau $\alpha$
• voordeel t.o.v. kritieke waarden
  • p-waarde is onafhankelijk van $\alpha$
  • gemakkelijker om test te herhalen voor verschillende $\alpha$ waarden

Een onderzoeker beschikt over normaalverdeelde gegevens en wil de volgende hypothese toetsen met $\alpha = 0.01$ en $\sigma_X = 16$: $H_0: \mu_X = 50$ vs. $H_1: \mu_X \neq 50$. Om de hypothese te toetsen trekt de onderzoeker een steekproef van 64 personen; het steekproefgemiddelde in deze steekproef bedraagt 44. Welke beslissing neem je? Voer de hypothesetoets uit o.b.v. de p-waarde.

• gegeven
  • $\alpha = 0.01$
  • $\sigma_X = 16$
  • $n = 64$
  • $\overline x = 44$
• gevraagd
  • hypothesetoetsing o.b.v. p-waarde
• oplossing
  • stap 1
    • $H_0: \mu_X = 50$
    • $H_1: \mu_X \neq 50$ (tweezijdig)
  • stap 2
    • $n = 64$
    • $\alpha = 0.01$
  • stap 3
    • $TS = \dfrac{\overline X - \mu_X}{\frac{\sigma_X}{\sqrt n}} \sim N(0, 1)$
  • stap 4
    • $ts = \dfrac{44 - 50}{16 / \sqrt{64}} = -3$
  • stap 5
    • $ts$ sterk verschillend van nul is verdacht, dus beide staarten
  • stap 6
    • $p = 2P(TS \leq -3) \in [0.002, 0.004]$
    • $p \leq \alpha$
    • dus verwerp $H_0$ op significantieniveau $0.01$

4.3 Tweezijdige toetsen via betrouwbaarheidsinterval (BI)

• $H_0: \mu_X = \mu_0$
• $H_1: \mu_X \neq \mu_0$
• bereken $(1-\alpha)$ BI voor $\mu_X$
• beslissing
  • $\mu_0 \in BI$: aanvaard $H_0$
  • $\mu_0 \not\in BI$: verwerp $H_0$
• werkt enkel voor tweezijdige testen

Een onderzoeker beschikt over normaalverdeelde gegevens en wil de volgende hypothese toetsen met $\alpha = 0.01$ en $\sigma_X = 16$: $H_0: \mu_X = 50$ vs. $H_1: \mu_X \neq 50$. Om de hypothese te toetsen trekt de onderzoeker een steekproef van 64 personen; het steekproefgemiddelde in deze steekproef bedraagt 44. Welke beslissing neem je? Voer de hypothesetoets uit m.b.v. een betrouwbaarheidsinterval.

• gegeven
  • $\alpha = 0.01$
  • $\sigma_X = 16$
  • $n = 64$
  • $\overline x = 44$
• gevraagd
  • hypothesetoetsing m.b.v. BI
• oplossing
  • opstellen BI
    • $z_{1-\frac{\alpha}{2}}^* = z_{0.995}^* = 2.5758$
    • $\overline x \pm 2.5758 \dfrac{\sigma_X}{\sqrt n}$
    • $= 44 \pm 2.5758 \dfrac{16}{\sqrt{64}}$
    • $= 44 \pm 5.1516$
    • $= [38.8484, 49.1516]$
  • beslissing
    • $50 \not\in BI$
    • verwerp $H_0$ op significantieniveau $0.01$

4.4 Eenzijdige toetsen

• stap 5
  • welke staart verdacht?
    • $H_1: \mu_X > \mu_0$
      • rechterstaart
    • $H_1: \mu_X < \mu_0$
      • linkerstaart
• stap 6
  • o.b.v. kritieke waarde
    • linkerstaart: $z_{\alpha}^*$
    • rechterstaart: $z_{1-\alpha}^*$
  • o.b.v. p-waarde
    • linkerstaart: $p = P(TS \leq ts)$
    • rechterstaart: $p = P(TS \geq ts)$
  • o.b.v. BI
    • (!) niet mogelijk

Een onderzoeker beschikt over normaalverdeelde gegevens en wil de volgende hypothese toetsen met $\alpha = 0.01$ en $\sigma_X = 16$: $H_0: \mu_X = 50$ vs. $H_1: \mu_X < 50$. Om de hypothese te toetsen trekt de onderzoeker een steekproef van 64 personen; het steekproefgemiddelde in deze steekproef bedraagt 44.

(a) Waaraan zijn $z^*$ en $ts$ gelijk? Welke conclusie trekt de onderzoeker?

(b) Hoeveel bedraagt de p-waarde? Wat is de conclusie van de onderzoeker?

• gegeven
  • $X \sim N(\ldots, 16^2)$
  • $\alpha = 0.01$
  • $\sigma_X = 16$
  • $n = 64$
  • $\overline x = 44$
• (a) gevraagd
  • $z^*$
  • $ts$
  • conclusie
• (a) oplossing
  • $z_{\alpha}^* = -2.3263$
  • $ts = \dfrac{44 - 50}{16 / \sqrt{64}} = -3$
  • verwerp $H_0$ op significantieniveau 0.01
• (b) gevraagd
  • p-waarde
  • conclusie
• (b) oplossing
  • $p = P(TS \leq -3) \in [0.001, 0.002]$
  • $p \leq \alpha$
  • verwerp $H_0$

5 Power

• soorten fouten
  • type 1 fout: $H_0 \text{ verwerpen} \mid H_0 \text{ waar}$
    • $P(\text{type 1 fout}) = \alpha$
  • type 2 fout: $H_0 \text{ aanvaarden} \mid H_0 \text{ vals}$
    • $P(\text{type 2 fout}) = \beta$
• power = onderscheidingsvermogen (OV) = $1 - \beta = P(H_0 \text{ verwerpen} \mid H_0 \text{ vals})$
• stappenplan
  • (1) hypothesetoetsing uitgaande van $H_0$
    • bepaal verwerpingsgebied
  • (2) bereken kans op verwerping uitgaande van waarheid

(1) Een onderzoeker wil de volgende hypothese toetsen, met $\alpha=0.05$: $H_0: \mu_X = 50$ vs. $H_1: \mu_X \neq 50$. Om de hypothese te toetsen trekt de onderzoeker een steekproef van 64 personen uit een normaalverdeelde populatie met $\sigma_X=16$. Voor welke waarden van het steekproefgemiddelde zal de onderzoeker $H_0$ aanvaarden?

• gegeven
  • $\alpha = 0.05$
  • $\sigma_X = 16$
  • $n = 64$
  • $X \sim N(\ldots, 16^2)$
• gevraagd
  • aanvaardingsgebied
• oplossing
  • o.b.v. kritieke waarden
    • alternatief: a.h.v. 95% BI voor $\mu_X$
  • stap 1
    • $H_0: \mu_X = 50$
    • $H_1: \mu_X \neq 50$ (tweezijdig)
  • stap 2
    • $n = 64$
    • $\alpha = 0.05$
  • stap 3
    • $Z = \dfrac{\overline X - \mu_X}{\frac{\sigma_X}{\sqrt n}} \sim N(0, 1)$
  • stap 4
  • stap 5
    • $z$ sterk verschillend van nul is verdacht, dus beide staarten
  • stap 6
    • $z_{\frac{\alpha}{2}}^* = -1.96$
    • $z_{1 - \frac{\alpha}{2}}^* = 1.96$
  • aanvaardingsgebied
    • $-1.96 < Z < 1.96$
    • $\iff \mu_X - 1.96\frac{\sigma_X}{\sqrt n} < \overline X < \mu_X + 1.96\frac{\sigma_X}{\sqrt n}$
    • $\iff 50 - 1.96\frac{16}{8} < \overline X < 50 + 1.96\frac{16}{8}$
    • $\iff 46.08 < \overline X < 53.92$

(2) Voortbouwend op de vorige even oefenen, hoeveel bedraagt het onderscheidingsvermogen als in werkelijkheid $\mu_X=44$?

• $H_0$ vals
• OV
  • $= 1 - P(H_0 \text{ aanvaarden} \mid H_0 \text{ vals})$
  • $= 1 - P(46.08 < \overline X < 53.92 \mid H_0 \text{ vals})$
  • $= 1 - P(\frac{46.08-44}{16 / \sqrt{64}} < Z < \frac{53.92 - 44}{16 / \sqrt{64}} \mid H_0 \text{ vals})$
  • $= 1 - P(1.04 < Z < 4.96)$
  • $= 1 - [P(Z < 4.96) - P(Z < 1.04)]$
  • $= 1 - [P(Z < 4.96) - P(Z < 1.04)]$
  • $\approx 1 - [1 - 0.85]$
  • $= 0.85$

5.1 Hoe power maximaliseren

• grotere $\alpha$
  • $H_0$ wordt sneller verworpen
• waarheid ligt verder weg van $H_0$, in richting $H_1$
• kleinere $\sigma_X$
• grotere $n$

5.2 Power in praktijk

• waarheid niet gekend tijdens experiment
• kies $n$ i.f.v. gewenste power en effectgrootte

6 t-toetsen

6.1 Inferentie voor het gemiddelde

• tot nu toe (z-toets): normaalmodel met gekende $\sigma_X$
  • $Z = \dfrac{\overline X - \mu_X}{\sigma_X / \sqrt n} \sim N(0, 1)$
• nieuw (t-toets): normaalmodel met onbekende $\sigma_X$
  • gebruik schatter $\hat\sigma_X = s'_x$
  • $T = \dfrac{\overline X - \mu_X}{S'_X / \sqrt n} \sim t_{df=n-1}$
  • verder exact zelfde aanpak voor BI en hypothesetoetsing
• student t-verdeling $t_{df}$
  • lijkt op standaardnormale verdeling
    • met iets dikkere staarten
  • $df$: degrees of freedom = vrijheidsgraden
    • $df \to \infty: t_{df} \to N(0, 1)$

6.2 Vergelijken van twee verwachtingen

• $H_0: \mu_X - \mu_Y = \mu_0$
  • speciaal geval: $H_0: \mu_X - \mu_Y = 0 \iff \mu_X = \mu_Y$
• $H_1: \mu_X - \mu_Y \neq \mu_0$ (of $<$ of $>$)

6.2.1 Afhankelijke steekproeven

• $n_X = n_Y$ is een nodige maar geen voldoende voorwaarde voor gepaarde steekproeven
• gebruik z-toets of t-toets voor $\mu_{X-Y} = \mu_X - \mu_Y$

6.2.2 Onafhankelijke steekproeven

6.2.2.1 Beide varianties bekend

• voorwaarden
  • $X$ en $Y$ onafhankelijk
  • $X$ en $Y$ beide normaal verdeeld
    • of benaderd normaal via centrale limietstelling ($n_X > 30, n_Y > 30$)
  • $\sigma_X$ en $\sigma_Y$ bekend
• onafhankelijk: $\sigma_{\overline X - \overline Y}^2 = \sigma_{\overline X}^2 + \sigma_{\overline Y}^2 = \frac{\sigma_X^2}{n_X} + \frac{\sigma_Y^2}{n_Y}$
• $Z = \dfrac{\overline X - \overline Y - (\mu_X - \mu_Y)}{\sqrt{\frac{\sigma_X^2}{n_X} + \frac{\sigma_Y^2}{n_Y}}} \sim N(0, 1)$

6.2.2.2 Beide varianties volledig onbekend

• voorwaarden
  • $X$ en $Y$ onafhankelijk
  • $X$ en $Y$ beide normaal verdeeld
    • of benaderd normaal via centrale limietstelling ($n_X > 30, n_Y > 30$)
  • beide met onbekende variantie
• Satterthwaite benadering
• $T = \dfrac{\overline X - \overline Y - (\mu_X - \mu_Y)}{\sqrt{\frac{S_X^{\prime 2}}{n_X} + \frac{S_Y^{\prime 2}}{n_Y}}} \sim t_{df=k}$
  • $k = \dfrac{\left(\frac{s_x^{\prime 2}}{n_X} + \frac{s_y^{\prime 2}}{n_Y}\right)^2}{\frac{1}{n_X - 1}\left(\frac{s_x^{\prime 2}}{n_X}\right)^2 + \frac{1}{n_Y-1}\left(\frac{s_y^{\prime 2}}{n_Y}\right)^2}$
    • afronden naar beneden

6.2.2.3 Beide varianties onbekend maar gelijk (homoscedasticiteit)

• voorwaarden
  • $X$ en $Y$ onafhankelijk
  • $X$ en $Y$ beide normaal verdeeld
    • of benaderd normaal via centrale limietstelling ($n_X > 30, n_Y > 30$)
  • beide met onbekende maar gelijke variantie: $\sigma_X = \sigma_Y$
• pooled estimator $\hat\sigma^2_{pooled}$
  • $= \dfrac{(n_X - 1)s_x^{\prime 2} + (n_Y-1)s_y^{\prime 2}}{n_X + n_Y -2}$
  • $= \dfrac{n_X s_x^2 + n_Y s_y^2}{n_X + n_Y -2}$
• $T = \dfrac{\overline X - \overline Y - (\mu_X - \mu_Y)}{\hat\sigma_{pooled} \sqrt{\frac{1}{n_X} + \frac{1}{n_Y}}} \sim t_{df=n_X+n_Y-2}$

7 Inferentie met andere grootheden dan het gemiddelde

7.1 Inferentie voor één fractie

• $H_0: \vartheta = \vartheta_0$
• $H_1: \vartheta \neq \vartheta_0$ (of $<$ of $>$)
• $X_i \sim Bern(\vartheta)$ (i.i.d.)
  • populatiefractie $\vartheta$ (parameter)
  • we hebben geen goede schatter voor deze parameter als $n=1$
  • dus herhaal experiment $n$ keer
• $Y = \sum_{i=1}^n X_i \sim Bin(n, \vartheta) \sim N(n\vartheta, n\vartheta(1 - \vartheta))$ (als $n$ groot genoeg)
  • zie hoorcollege 2
• $\overline X = \frac{1}{n}\sum_{i=1}^n X_i = \frac{Y}{n} \sim N(\vartheta, \frac{\vartheta(1-\vartheta)}{n})$ (als $n$ voldoende groot)
  • gebruik steekproefproportie $\hat\vartheta$ als schatter
    • TS = PROP $= \overline X = \hat\vartheta$
      • $Z = \dfrac{\overline X - \vartheta_0}{\sqrt{\frac{\vartheta_0(1-\vartheta_0)}{n}}} \sim N(0, 1)$
    • ts = prop $= \overline x$
      • $z = \dfrac{\overline x - \vartheta_0}{\sqrt{\frac{\vartheta_0(1-\vartheta_0)}{n}}}$
• voorwaarden (herhaling)
  • $n\vartheta \geq 10$ en $n(1 - \vartheta) \geq 10$
• keuze succes vs mislukking maakt niet uit
  • omwisselen geeft zelfde conclusie

Het stadsbestuur claimt dat 92% van de inwoners regelmatig het openbaar vervoer gebruikt om naar het werk te gaan. Een stedenbouwkundige denkt dat dit percentage in werkelijkheid lager ligt. Om dit te testen ondervraagt hij 200 mensen, 87% van hen geeft aan regelmatig het openbaar vervoer te gebruiken. Gegeven $\alpha = 0.01$, test of de stedenbouwkundige gelijk heeft d.m.v. de $p$-waarde.

• gegeven
  • $n=200$
  • $\vartheta_0 = 0.92$
  • $prop = \overline x = 0.87$
  • $\alpha = 0.01$
• gevraagd
  • hypothesetoets d.m.v. $p$-waarde
• oplossing
  • check voorwaarden
    • $n\vartheta = 184 \geq 10$
    • $n(1 - \vartheta) = 16 \geq 10$
  • stap 1
    • $H_0: \vartheta = 0.92$
    • $H_1: \vartheta < 0.92$
  • stap 2
    • $n = 200$
    • $\alpha = 0.01$
  • stap 3
    • $Z = \dfrac{\overline X - 0.92}{0.0192} \sim N(0, 1)$
  • stap 4
    • $z = \dfrac{0.87 - 0.92}{0.0192} \approx -2.6064$
  • stap 5
    • linkerstaart verdacht
  • stap 6
    • $p = P(Z < -2.6064)$
    • $0.004 < p < 0.005$
    • $p < \alpha \implies$ verwerp $H_0$

Een vader heeft 8 zonen en 0 dochters. Hij wil de hypothese toetsen dat de kans op een meisje verschillend is van kans op jongen. Welke van onderstaande uitspraken is correct?

• gegeven
  • $n = 8$
  • $prop = \frac{8}{8} = 1$
• gevraagd
  • $p$-waarde
• oplossing
  • $H_0: \vartheta = 0.50$
  • $H_1: \vartheta \neq 0.50$
  • check voorwaarden
    • $n\vartheta = 4 < 10$ -> niet voldaan onder $H_0$
    • dus we mogen geen normale benadering gebruiken
    • dus gebruik exacte binomiale kans
  • $Y \sim Bin(8, 0.5)$
  • $p = P(Y \geq 8) = P(Y=8) = \binom{8}{8} 0.5^8 (1-0.5)^0 \approx 0.0039$

7.1.1 Betrouwbaarheidsintervallen

• voorwaarden (herhaling)
  • $n\vartheta \geq 10$ en $n(1 - \vartheta) \geq 10$
  • gebruik populatiecorrectiefactor indien nodig ($N < 20n$)
• gebruik $prop$ als schatting voor $\vartheta$
  • gevolg: BI niet meer equivalent met tweezijdige hypothesetoets
• BI
  • $prop \pm z^* \sqrt{\dfrac{prop(1-prop)}{n}}$
• foutenmarge vs $n$
  • $m = z^* \sqrt{\dfrac{prop(1-prop)}{n}}$
  • kies $n \geq (\frac{z^*}{m})^2 \cdot prop \cdot (1 - prop)$
    • zodat foutenmarge maximaal $m$ is
    • $prop$ ongekend?
      • zoek in literatuur
      • of gebruik $prop = 0.5$ (geeft grootst mogelijke $n$)

Een departement psychologie vermoedt dat onder hun studenten een significant percentage problematische angst ervaart. Het departement telt in totaal 5000 studenten. Om het percentage studenten dat met angst kampt te schatten, ondervraagt men 300 verschillende studenten. 120 onder hen rapporteren met angst te kampen. Geef een 95% betrouwbaarheidsinterval van de fractie psychologiestudenten aan dit departement die angstproblemen hebben.

• gegeven
  • $\vartheta$: fractie psychologiestudenten met angstproblemen
  • $N = 5000$
  • $n= 300$
  • $prop = \frac{120}{300} = 0.4$
  • $\alpha = 0.05$
• gevraagd
  • 95% BI
• oplossing
  • check voorwaarden
    • $n\vartheta \geq 10$ en $n(1 - \vartheta) \geq 10$
      • OK (o.b.v. $prop$)
    • $N < 20n$
      • dus gebruik correctiefactor $\sqrt{\frac{N-n}{N-1}} \approx \sqrt{0.9402} \approx 0.9696$
  • $z^*_{0.975} = 1.96$
  • $prop \pm z^* \cdot \sqrt{\frac{N-n}{N-1}} \cdot \sqrt{\dfrac{prop(1-prop)}{n}}$
  • $\approx 0.4 \pm 1.96 \cdot 0.9696 \cdot 0.0283$
  • $\approx 0.4 \pm 0.0538$
  • $\approx [0.3462, 0.4538]$

Een onderzoeker wil het percentage leerlingen in het basisonderwijs schatten dat regelmatig gepest wordt op school. Hij wil dit doen aan de hand van een 99% BI voor de fractie gepeste leerlingen. Hoeveel leerlingen moet hij minstens betrekken in zijn onderzoek als de foutmarge hoogstens 1% mag bedragen?

Ga er hierbij van uit dat het percentage leerlingen dat gepest wordt in het basisonderwijs ongeveer gelijk is aan het percentage leerlingen dat gepest wordt in het secundair onderwijs (15%).

• gegeven
  • $\vartheta$: fractie gepeste leerlingen
  • $\alpha = 0.01$
  • $prop = 0.15$
• gevraagd
  • minimale $n$ voor $m=0.01$
• oplossing
  • $z^*_{0.995} = 2.5758$
  • $n$
    • $\geq (\frac{z^*}{m})^2 \cdot prop \cdot (1 - prop)$
    • $\geq (\frac{2.5758}{0.01})^2 \cdot 0.15 \cdot 0.85$
    • $\geq 8459.3007$
  • dus $n \geq 8460$

7.2 Vergelijken van twee fracties

• van twee onafhankelijke groepen: $A$ en $B$
• voorwaarden
  • ZTW of grote populatie ($20n \leq N$)
  • minstens 10 successen en 10 mislukkingen in beide steekproeven
• $H_0: \vartheta_A = \vartheta_B$
• $H_!: \vartheta_A \neq \vartheta_B$ (of $<$ of $>$)
• $TS = PROP_A - PROP_B \sim N(\vartheta_A - \vartheta_B, \frac{\vartheta_A(1-\vartheta_A)}{n_A} + \frac{\vartheta_B(1-\vartheta_B)}{n_B})$
• pooled estimate: $\hat\vartheta = \dfrac{n_A prop_A + n_B prop_B}{n_A + n_B}$
• $Z = \dfrac{PROP_A - PROP_B}{\sqrt{\hat\vartheta(1-\hat\vartheta)(\frac{1}{n_A} + \frac{1}{n_B})}} \sim N(0, 1)$ onder $H_0$
• BI: $prop_A - prop_B \pm z^* \sqrt{\dfrac{prop_A(1-prop_A)}{n_A} + \dfrac{prop_B(1-prop_B)}{n_B}}$

Is er een significant verschil in alcoholmisbruik tussen mannen en vrouwen? Je neemt een steekproef met 7180 mannen en 9916 vrouwen, waarvan 1630 mannen en 1684 vrouwen te veel alcohol consumeren.

(a) Wat beslis je op basis van een 95% BI?

(b) En op basis van de p-waarde van een significantietoets ($\alpha=0.05$)?

• gegeven
  • $n_M = 7180$
  • $n_V = 9916$
  • $prop_M = \frac{1630}{7180} \approx 0.2270$
  • $prop_V = \frac{1684}{9916} \approx 0.1698$
• gevraagd (a)
  • 95% BI
• oplossing (a)
  • $z^*_{0.975} = 1.96$
  • $prop_A - prop_B \pm z^* \sqrt{\dfrac{prop_A(1-prop_A)}{n_A} + \dfrac{prop_B(1-prop_B)}{n_B}}$
  • $\approx 0.0572 \pm 1.96 \cdot 0.0062$
  • $[0.0450, 0.0694]$
  • conclusie
    • $0$ niet in interval
    • fracties significant verschillend
• gevraagd (b)
  • o.b.v. p-waarde
• oplossing (b)
  • check voorwaarden
    • ✅ grote populatie ($20n \leq N$)
    • ✅ minstens 10 successen en 10 mislukkingen in beide steekproeven
  • stap 1
    • $H_0: \vartheta_M = \vartheta_V$
    • $H_1: \vartheta_M \neq \vartheta_V$
  • stap 2
    • $n_M = 7180$
    • $n_V = 9916$
    • $\alpha = 0.05$
  • stap 3
    • $\hat\vartheta = \dfrac{n_A prop_A + n_B prop_B}{n_A + n_B} = \dfrac{1630+1684}{7180+9916} \approx 0.1938$
    • $Z = \dfrac{PROP_A - PROP_B}{\sqrt{\hat\vartheta(1-\hat\vartheta)(\frac{1}{n_A} + \frac{1}{n_B})}} \sim N(0, 1)$ onder $H_0$
      • $= \dfrac{PROP_A - PROP_B}{0.0061}$
  • stap 4
    • $z = \dfrac{0.2270 - 0.1698}{0.0061} \approx 9.3377$
  • stap 5
    • beide staarten verdacht
  • stap 6
    • $p = 2P(Z > 9.3377) < 2 \cdot 0.0005 = 0.001$
    • $p < \alpha \implies$ verwerp $H_0$

7.3 Inferentie voor populatiespreiding

• o.b.v. chi kwadraat ($\chi^2$) verdeling
  • opgelet: asymmetrisch
• ter herinnering: $\dfrac{n}{n-1} S_X^2 = S_X^{\prime 2}$
• voorwaarden
  • $X \sim N(\mu_X, \sigma_X^2)$
• $TS = \dfrac{(n-1)S_X^{\prime 2}}{\sigma_X^2} = \dfrac{nS_X^2}{\sigma_X^2} \sim \chi_{df=n-1}^2$ onder $H_0$
• BI: $\sigma_X^2 \in \left[\dfrac{nS_X^2}{x^*_{\frac{\alpha}{2}}}, \dfrac{nS_X^2}{x^*_{1-\frac{\alpha}{2}}}\right]$

Een fabriek produceert vijzen die een diameter van 5 mm horen te hebben. De maximaal toegelaten variantie in diameter is 0.01 mm². Om zeker te zijn dat er geen problemen zijn met het productieproces wordt er een kwaliteitscontrole gedaan: er wordt een steekproef van 20 vijzen getrokken. De variantie $s^{\prime 2}$ binnen deze steekproef blijkt gelijk te zijn aan 0.015mm². Is er een probleem in de fabriek?

• gegeven
  • $X$: diameter vijzen (in mm)
  • $\sigma_0^2 = 0.010$
  • $n = 20$
  • $s_x^{\prime 2} = 0.015$
• gevraagd
  • probleem in fabriek? moeten we $H_0$ verwerpen?
• oplossing
  • check voorwaarden
    • extra assumptie: $X \sim N$
  • stap 1
    • $H_0: \sigma_X^2 = 0.010$
    • $H_1: \sigma_X^2 > 0.010$
  • stap 2
    • $n = 20$
    • $\alpha = ?$
  • stap 3
    • $TS = \dfrac{19 S_X^{\prime 2}}{0.010} = 1900S_X^{\prime 2} \sim \chi_{df=19}^2$ onder $H_0$
  • stap 4
    • $ts = 1900 \cdot 0.015 = 28.5$
  • stap 5
    • rechterstaart verdacht
  • stap 6
    • $p = P(TS > 28.5)$
    • $0.05 < p < 0.10$
    • dus $H_0$ niet verwerpen voor meest gangbare waarden van $\alpha$
    • dus geen probleem in fabriek

7.4 Vergelijken van twee populatiestandaarddeviaties (F-toets)

• voorwaarden
  • $s_x \approx s_y$
  • $X \sim N$
  • $Y \sim N$
  • $X, Y$ onafhankelijk
• $H_0: \sigma_X = \sigma_Y \iff \dfrac{\sigma_Y}{\sigma_X} = 1$
• $H_1: \sigma_X \neq \sigma_Y$
• $TS = \dfrac{S^{\prime 2}_X}{S^{\prime 2}_Y} \dfrac{\sigma_Y^2}{\sigma_X^2} \sim F_{df_1=n_X-1, df_2=n_Y-1}$
  • opgelet: $F$ verdeling is asymmetrisch
    • belangrijk om met kleinste staart te werken voor $p$-waarden
    • bepaal a.h.v. mediaan
      • $ts$ onder mediaan: links kleiner
      • $ts$ boven mediaan: rechts kleiner
• wat als we teller en noemer omwisselen?
  • dan ook $df_1$ en $df_2$ omwisselen
  • beslissing blijft hetzelfde

Een onderzoeker wil nagaan of studenten pedagogie meer variëren in hoeveel geld ze uitgeven tijdens een avondje stappen in Leuven dan studenten logopedie. Hieronder zie je wat gegevens hierover.

Studierichting	$n$	gemiddelde	$s^{\prime 2}$
Pedagogie (P)	51	8.6667	3.1535
Logopedie (L)	201	7.6235	2.1023

Hoeveel bedraagt $p$?

• gegeven
  • gemiddeldes (niet belangrijk)
  • $s^{\prime 2}_p = 3.1535$
  • $s^{\prime 2}_l = 2.1023$
  • $n_P = 51$
  • $n_L = 201$
• gevraagd
  • $p$ waarde
• oplossing
  • stap 1
    • $H_0: \sigma_P = \sigma_L$
    • $H_1: \sigma_P > \sigma_L$ (eenzijdig)
  • stap 2
    • $n_P = 51$
    • $n_L = 201$
  • stap 3
    • $TS = \dfrac{S^{\prime 2}_P}{S^{\prime 2}_L} \dfrac{\sigma_L^2}{\sigma_P^2} \sim F_{50, 200}$
  • stap 4
    • $ts = \dfrac{s^{\prime 2}_p}{s^{\prime 2}_l} = 1.5000$
  • stap 5
    • rechterstaart verdacht
  • stap 6
    • $p = P(TS > 1.5) = 1-P(TS \leq 1.5)$
    • $0.025 < p < 0.050$

8-9 Niet-parametrische statistiek

• niet-parametrisch = verdelingsvrij
• geschikt voor
  • kleine steekproeven
  • niet-numerieke data
  • scheve verdelingen of uitschieters

8 Werken met geobserveerde scores

8.1 Bootstrapmethode

• trek originele steekproef uit populatie
• trek herhaaldelijk met teruglegging bootstrapsteekproeven uit originele steekproef
  • allemaal even groot als originele steefproef
• bereken verdeling van statistiek over deze bootstrapsteekproeven heen
• geschikt voor
  • gemiddelde, regressiecoefficienten ($\beta_0, \beta_1$)
• minder geschikt voor
  • kleine $n$
  • kwantielen (incl. mediaan)

Gegeven dat je volgende steekproef hebt geobserveerd: $7, 5, 8, 1, 4$, om iets te zeggen over $\mu$. Welk van volgende steekproeven is dan een geldige bootstrapsteekproef?

• (A) 4, 8, 1, 7
• (B) 3, 1, 4, 8, 7
• (C) 7, 8, 8, 1, 4, 5
• (D) 7, 1, 1, 4, 5

• (A) ongeldig, $n < 5$
• (B) ongeldig, $3$ komt niet uit originele steefproef
• (C) ongeldig, $n > 5$
• (D) geldig

Hoe ga je concreet te werk als je twee onafhankelijke steekproeven hebt en je iets wil besluiten over het verschil in populatiegemiddelde tussen de twee corresponderende groepen?

• (A) ik doe alle scores in 1 bak, trek ZTL evenveel scores en steek ze random in groep 1 en groep 2
• (B) Ik doe alle scores in 1 bak, trek MTL evenveel scores en steek ze random in groep 1 en groep 2
• (C) Ik doe de scores van groep 1 in een bak en de scores van groep 2 in een tweede bak. Voor groep 1 trek ik ZTL evenveel scores uit bak 1 en voor groep 2 trek ik ZTL evenveel scores uit bak 2
• (D) Ik doe de scores van groep 1 in een bak en de scores van groep 2 in een tweede bak. Voor groep 1 trek ik MTL evenveel scores uit bak 1 en voor groep 2 trek ik MTL evenveel scores uit bak 2.

• (D)

8.2 Permutatietoets

8.2.1 Onafhankelijke groepen

• groep $A$ en groep $B$
• TS: $\overline X_A - \overline X_B$
  • $\neq \overline{X_A - X_B}$
• ts: $\overline x_A - \overline x_B$
• $H_0: \mu_A = \mu_B$
  • als $H_0$ waar is, maakt het niet uit in welke groep een observatie zit
  • bereken alle mogelijke permutatiesteekproeven
    • aantal = $\dbinom{n_A+n_B}{n_A} = \dbinom{n_A+n_B}{n_B}$
  • bereken $p$-waarde o.b.v. deze geschatte steekproevenverdeling van $\overline X_A - \overline X_B$
    • eenzijdige alternatieve hypothese: oppervlakte verdachte staart
    • tweezijdige alternatieve hypothese: tweemaal oppervlakte kleinste staart

Wat als we een extra proefpersoon toevoegen aan controleconditie: de controleconditie (C) bevat dan 5 personen, de behandelingsconditie (B) 4. Hoeveel permutaties zijn er mogelijk?

• $\dbinom{5+4}{4} = \dbinom{5+4}{5} = 126$

Toets de hypothese $\mu_B > \mu_C$. Hoeveel bedraagt de $p$-waarde?

Controle	Behandeling
1	10
7	9
3	5
0	8
2

• $\overline c = 2.6$
• $\overline b = 8$
• $ts = \overline b - \overline c = 5.4$
• $p = P(TS \geq 5.4) = \frac{2}{126} \approx 0.0159$
  • incl. originele steekproef
  • slechts 1 andere permutatiesteekproef met groter verschil:

Controle	Behandeling
1	10
5	9
3	7
0	8
2

8.2.2 Afhankelijke groepen

• $X_1$ en $X_2$
• $TS = \overline{X_1 - X_2}$
• $ts = \overline{x_1 - x_2}$
• $H_0: \mu_{X_1 - X_2} = 0$
  • als $H_0$ waar is, kunnen resultaten per observatie omgewisseld worden
    • dus het verschil verandert van teken want $x_1 - x_2 = -(x_2 - x_1)$
  • bereken alle mogelijke permutatiesteekproevenn
    • aantal = $2^n$
  • bereken gemiddelde verschilscore $ts$ voor elke permutatiesteekproef
  • bereken $p$-waarde o.b.v. deze geschatte steekproevenverdeling van $\overline{X_1 - X_2}$
    • eenzijdige alternatieve hypothese: oppervlakte verdachte staart
    • tweezijdige alternatieve hypothese: tweemaal oppervlakte kleinste staart

We willen toetsen of tweelingen significant verschillen in lichaamslengte ($\alpha=0.05$). Hoeveel bedraagt de tweezijdige $p$-waarde, gegeven onderstaande data van 8-jarige tweelingen?

Tweeling	Lengte oudste kind (cm)	Lengte jongste kind (cm)	Verschil $x_1-x_2$
1	145	138	+7
2	140	136	+4
3	144	147	−3
4	144	139	+5
5	142	143	−1
6	147	141	+6

• gevraagd
  • tweezijdige $p$-waarde
• oplossing
  • $H_0: \mu_{X_1 - X_2} = 0$
  • $H_1: \mu_{X_1 - X_2} \neq 0$
  • $n = 6$
  • aantal permutaties: $2^n = 64$
  • tweezijdige $p$-waarde, dus teller moet een even getal zijn
    • schrap antwoorden (B) en (C)
  • $ts = \overline{x_1 - x_2} = \frac{18}{6} > 0$
    • dus oudste kind is gemiddeld groter
    • dus rechterstaart is de kleinste
  • zoek permutaties waarbij oudste kind gemiddeld 3cm of meer groter is
    • antwoord (A) kan enkel als de gegeven tabel al het meeste extreme verschil geeft -> schrappen
    • antwoord (D) moet correct zijn
    • $p = 2 \cdot P(TS \geq \frac{18}{6}) = 2 \cdot \frac{5}{64} = \frac{10}{64}$

Tweeling	Verschil
1	+7
2	+4
3	-3
4	+5
5	−1
6	+6
$ts$	18/6

Tweeling	Verschil
1	+7
2	+4
3	+3
4	+5
5	−1
6	+6
$ts$	24/6

Tweeling	Verschil
1	+7
2	+4
3	-3
4	+5
5	-1
6	+6
$ts$	20/6

Tweeling	Verschil
1	+7
2	+4
3	+3
4	+5
5	-1
6	+6
$ts$	26/6

Tweeling	Verschil
1	+7
2	-4
3	+3
4	+5
5	-1
6	+6
$ts$	18/6

9 Werken met kenmerk van de scores

9.1 Onafhankelijke groepen

9.1.1 Wilcoxon rangsomtoets

• groep $A$ en groep $B$
• $n = n_A + n_B$
• $H_0: A = B$
• maak tabel met kolommen $X$, rang, groep, gesorteerd op $X$ oplopend
  • knopen = ties
    • neem gemiddelde van rangen
• $TS = W_A$: som van rangen uit groep $A$
  • kan ook a.h.v. $W_B$
• benaderende methode
  • voorwaarden
    • $n_A \geq 10$
    • $n_B \geq 10$
  • $W_A \sim N(\mu_{W_A}, \sigma_{W_A}^2) \iff \frac{W_A - \mu_{W_A}}{\sigma_{W_A}} \sim N(0,1)$ onder $H_0$
    • $\mu_{W_A} = \dfrac{n_A \cdot (n+1)}{2}$
    • $\sigma_{W_A}^2 = \dfrac{n_A \cdot n_B \cdot (n+1)}{12}$
    • denk aan continuiteitscorrectie
• exacte methode
  • = permutatietoets op rangnummers i.p.v. op waarden
  • want onder $H_0$ zijn rangnummers inwisselbaar over groepen
  • aantal permutaties: $\dbinom{n_A+n_B}{n_A}$

Gegeven onderstaande data, hoeveel bedraagt $w_B$?

• Controle (C): 1, 6, 5, 3
• Behandeling (B): 7, 4, 9, 10

• $w_B = 3 + 6 + 7 + 8 = 24$

$X$	rang	groep
1	1	C
3	2	C
4	3	B
5	4	C
6	5	C
7	6	B
9	7	B
10	8	B

Hoeveel bedragen de exacte en benaderende $p$-waarden bij een tweezijdige toets?

• benaderend
  • merk op: voorwaarden geschonden ($n_A > 10, n_B > 10$)
  • $\mu_{W_B} = \dfrac{n_B \cdot (n+1)}{2} = 18$
    • $24 > 18$, dus rechterstaart verdacht
  • $\sigma_{W_B}^2 = \dfrac{n_B \cdot n_C \cdot (n+1)}{12} = 12$
  • $\dfrac{W_B - 18}{\sqrt{12}} \sim N(0,1)$
  • $p$
    • $= 2P(W_B \geq 23.5)$ (continuiteitscorrectie)
    • $= 2(1 - P(W_B < 23.5))$
    • $= 2\left(1 - P\left(\dfrac{W_B - 18}{\sqrt{12}} < \dfrac{23.5 - 18}{\sqrt{12}}\right)\right)$
    • $= 2\left(1 - \Phi_Z^{-1}\left(\dfrac{5.5}{\sqrt{12}}\right)\right)$
    • $\iff 2 (1 - 0.945) < p < 2 (1 - 0.940)$
    • $\iff 0.11 < p < 0.12$
• exact (permutatietoets op rangen)
  • $\dbinom{4+4}{4} = 70$
  • combinaties van rangen $\geq 24$
    • 8 + 7 + 6 + 5 = 26
    • 8 + 7 + 6 + 4 = 25
    • 8 + 7 + 6 + 3 = 24
    • 8 + 7 + 5 + 4 = 24
  • $p = 2 \cdot \dfrac{4}{70} = \dfrac{8}{70} \approx 0.1143$

9.2 Afhankelijke groepen

9.2.1 Wilcoxon rangtekentoets

• bereken verschilscores $x_1 - x_2$
• schrap koppels met $x_1 = x_2$
• sorteer volgens $|x_1-x_2|$ oplopend
  • knopen = ties
    • neem gemiddelde van rangen
• bereken rang en signed rang
• $W^+ =$ som van rangnummers van positieve verschilscores ($\in \mathbb N$)
• $W^- =$ som van rangnummers van negatieve verschilscores ($\in \mathbb N$)
• $H_0$: verschilscores symmetrisch verdeeld rond nul (mediaan is nul)
• benaderende methode
  • voorwaarden
    • $n$ niet te klein
  • $W^+ \sim N(\mu_{W^+}, \sigma_{W^+}^2) \iff \dfrac{W^+ - \mu_{W^+}}{\sigma_{W^+}} \sim N(0,1)$ onder $H_0$
    • $\mu_{W^+} = \dfrac{n \cdot (n+1)}{4}$
    • $\sigma_{W^+}^2 = \dfrac{n \cdot (n+1) \cdot (2n+1)}{24}$
    • denk aan continuiteitscorrectie
• exacte methode
  • = permutatietoets op rangnummers i.p.v. op waarden
  • want onder $H_0$ zijn rangnummers inwisselbaar binnen koppels
  • aantal permutaties: $2^n$ (na schrappen van koppels met gelijke scores)

Hoeveel bedraagt $W^+$ bij de rangtekentoets om na te gaan of tweelingen significant verschillen in lichaamslengte ($\alpha=0.05$)?

Tweeling	Lengte oudste kind (cm)	Lengte jongste kind (cm)	Verschil	Rang	Signed rank
1	142	138
2	140	136
3	144	147
4	144	139
5	142	143
6	146	141
7	149	143
8	150	145
9	142	136
10	148	146

Tweeling	Lengte oudste kind (cm)	Lengte jongste kind (cm)	Verschil	Rang	Signed rank
5	142	143	-1	1	-1
10	148	146	2	2	+2
3	144	147	-3	3	-3
1	142	138	4	4.5	+4.5
2	140	136	4	4.5	+4.5
4	144	139	5	7	+7
6	146	141	5	7	+7
8	150	145	5	7	+7
7	149	143	6	9.5	+9.5
9	142	136	6	9.5	+9.5

• $W^+ = 2 + 4.5 + 4.5 + 7 + 7 + 7 + 9.5 + 9.5 = 51$

9.2.2 Gepaarde tekentoets

• kijk enkel naar teken van verschil en niet naar grootte
• voordelen
  • robuuster tegen uitbijters
  • ook geschikt voor kwalitatieve data
• schrap koppels met $x_1 = x_2$
• $\vartheta = P(\text{observeer positieve verschilscore})$
• $H_0$: geen effect, dus $\vartheta = 0.5$
• $TS$: aantal positieve verschilscores
• $TS \sim Bin(n, 0.50)$ onder $H_0$

Hoeveel bedraagt de $p$-waarde bij de tekentoets om na te gaan of tweelingen significant verschillen in lichaamslengte?

Tweeling	Lengte oudste kind (cm)	Lengte jongste kind (cm)	Verschil
1	142	138
2	140	136
3	144	147
4	144	139
5	142	143
6	146	141
7	149	143
8	150	145
9	142	136
10	148	146

Tweeling	Lengte oudste kind (cm)	Lengte jongste kind (cm)	Verschil
1	142	138	+
2	140	136	+
3	144	147	-
4	144	139	+
5	142	143	-
6	146	141	+
7	149	143	+
8	150	145	+
9	142	136	+
10	148	146	+

• tweezijdig
• $ts = 8$
• $TS \sim Bin(10, 0.50)$
  • $\mu = n\vartheta = 10 \cdot 0.5 = 5$
  • $ts > \mu$, dus rechterstaart verdacht
• $p = 2P(TS \geq 8) = 2(P(TS = 8) + P(TS = 9) + P(TS = 10))$
  • $P(TS = 8) = \dbinom{10}{8} 0.5^8 (1-0.5)^2 \approx 0.0439$
  • $P(TS = 9) = \dbinom{10}{9} 0.5^9 (1-0.5) \approx 0.0098$
  • $P(TS = 10) = \dbinom{10}{10} 0.5^10 \approx 0.0010$
  • $2P(TS \geq 8) \approx 0.1094$

10 Goodness of fit

• $H_0$: vooropgesteld model is houdbaar
• $H_1$: vooropgesteld model is onhoudbaar
• m.b.v. $\chi^2$ verdeling
  • $\chi^2_{df=k} = \sum_{i=1}^k Z_i^2 \mid Z_i \sim N(0, 1)$ i.i.d.

10.1 Twee onafhankelijke Bernouilli variabelen

• $X \sim Bern(\vartheta_X)$
• $Y \sim Bern(\vartheta_Y)$
• $I$: aantal categorieen
  • hier: $I = 2 \cdot 2 = 4$
  • $\{(0,0), (0,1), (1,0), (1,1)\}$
• per categorie $i$
  • observed waarde $O_i$
  • expected waarde $E_i$
• $TS = X^2 = \sum_{i=1}^I \dfrac{(O_i - E_i)^2}{E_i} \sim \chi^2_{df=I-1-k}$ onder $H_0$
  • $k$: aantal geschatte parameters uit geobserveerde gegevens
    • hier: $k=2$
      • $\hat\vartheta_X = prop_x$
      • $\hat\vartheta_Y = prop_y$
  • model onhoudbaar?
    • dan grotere verschillen tussen $E_i$ en $O_i$
    • dus grotere $X^2$
    • dus steeds rechterstaart verdacht
• voorwaarden
  • in theorie: $n$ oneindig groot
  • in praktijk: $\forall i: E_i \geq 5$
    • anders categorieen samenvoegen
• toepassing: test onafhankelijkheid
  • expected
    • $p_{X,Y}(x, y) = p_X(x) \cdot p_Y(y)$
    • $freq_X(x) = n \cdot p_X(x)$
• equivalent aan z-toets voor twee populatiefracties
  • $P(X^2 \geq ts) = 2P(Z \geq z)$ met $ts = z^2$
  • $x_{1-\alpha}^* = \left(z_{1-\frac{\alpha}{2}}^*\right)^2$
  • enkel voor $2 \times 2$ tabellen

• $X$: opleidingsgraad moeder
• $Y$: kinderen naar methodeschool

Methodeschool	Geen hoger onderwijs	Hoger onderwijs	Totaal
nee (0)	1243	1089	2332
ja (1)	51	205	256
Totaal	1294	1294	2588

Is er een verband tussen de opleidingsgraad van de moeder en of haar kinderen al dan niet naar een methodeschool gaan?

• gegeven
  • $n = 2588$
  • $prop_x = \frac{1294}{2588} = 0.5$
  • $prop_y = \frac{256}{2588} \approx 0.0989$
• gevraagd
  • $X, Y$ afhankelijk?
• oplossing
  • tabel voor $E_i$ opstellen
  • $E_{0,0} = n \cdot (1-prop_x) \cdot (1-prop_y) = 1166$
  • of $E_{0,0} = \dfrac{\text{kolomtotaal} \cdot \text{rijtotaal}}{\text{totaal}} = \dfrac{1294 \cdot 2332}{2588} = 1166$

Methodeschool	Geen hoger onderwijs	Hoger onderwijs	Totaal
nee	$\frac{1294 \cdot 2332}{2588} = 1166$	$\frac{1294 \cdot 2332}{2588} = 1166$	2332
ja	$\frac{1294 \cdot 256}{2588} = 128$	$\frac{1294 \cdot 256}{2588} = 128$	256
Totaal	1294	1294	2588

• oplossing (vervolg)
  • check voorwaarden
    • ✅ $\forall i: E_i > 5$
  • stap 1
    • $H_0:$X, Y$ onafhankelijk
    • $H_1:$X, Y$ afhankelijk
  • stap 2
    • $n = 2588$
    • $\alpha = ?$
  • stap 3
    • $TS = X^2 = \sum_{i=1}^I \dfrac{(O_i - E_i)^2}{E_i} \sim \chi^2_{df=I-1-k}$
      • $df = 4 - 1- 2 = 1$
  • stap 4
    • $ts = \dfrac{(1243 - 1166)^2}{1166} + \dfrac{(1089 - 1166)^2}{1166} + \dfrac{(51 - 128)^2}{128} + \dfrac{(205 - 128)^2}{128} = 102.8104$
  • stap 5
    • rechterstaart verdacht
  • stap 6
    • $p = P(X^2 > 102.8104) < 0.0005$
    • conclusie
      • verwerp $H_0$
      • dus $X, Y$ afhankelijk

Bepaal de 𝑧-waarde voor een toetsing van het verschil tussen de fracties kinderen die niet naar een methodeschool gaan conditioneel op het opleidingsniveau van de moeder.

• gegeven
  • groep A: moeder geen hoger onderwijs ($X=0$)
  • groep B: moeder wel hoger onderwijs ($X=1$)
  • $n = 2588$
    • $n_A = 1294$
    • $n_B = 1294$
  • $prop_a = \frac{1243}{1294} \approx 0.9606$
  • $prop_b = \frac{1089}{1294} \approx 0.8416$
• gevraagd
  • z-waarde voor toetsing verschil fracties
• oplossing
  • check voorwaarden
    • ✅ grote populatie ($20n \leq N$)
    • ✅ minstens 10 successen en 10 mislukkingen in beide steekproeven
  • stap 1
    • $H_0: \pi_{Y \mid X=0}(0) = \pi_{Y \mid X=1}(0) \iff 1-\vartheta_A = 1-\vartheta_B \iff \vartheta_A = \vartheta_B$
    • $H_1: \pi_{Y \mid X=0}(0) \neq \pi_{Y \mid X=1}(0)$
  • stap 2
    • $n_A = 1294$
    • $n_B = 1294$
    • $\alpha = ?$
  • stap 3
    • pooled estimate: $\hat\vartheta = \dfrac{n_A prop_A + n_B prop_B}{n_A + n_B} = \dfrac{1243 + 1089}{1294 + 1294} \approx 0.9011$
    • $Z$
      • $= \dfrac{PROP_A - PROP_B}{\sqrt{\hat\vartheta(1-\hat\vartheta)(\frac{1}{n_A} + \frac{1}{n_B})}} \sim N(0, 1)$ onder $H_0$
      • $\approx \dfrac{PROP_A - PROP_B}{0.0117}$
  • stap 4
    • $z \approx \dfrac{\frac{1243}{1294} - \frac{1089}{1294}}{0.0117} \approx 10.1395$
    • ✅ dubbelcheck $z^2 \approx 102.8104$

10.2 Twee onafhankelijke kwalitatieve variabelen

• $X$ met $m$ verschillende waarden $x_1, \ldots, x_j, \ldots, x_m$
• $Y$ met $m'$ verschillende waarden $y_1, \ldots, y_{j'}, \ldots, y_{m'}$
• zelfde principe als in 10.1
  • $TS = X^2 = \sum_{i=1}^I \dfrac{(O_i - E_i)^2}{E_i} \sim \chi^2_{df=I-1-k}$ onder $H_0$
  • $I = m \cdot m'$
  • $k = (m-1) + (m'-1) = m + m' -2$
  • $df = I - 1 - k = m \cdot m' - m - m' + 1 = (m-1)(m'-1)$

Er zijn 2 basisscholen die leerlingen leveren aan een secundaire school. Men gaat na in welke stroom (ASO, BSO, TSO, KSO) deze leerlingen terechtkomen. Hieronder vind je een kruistabel met de gegevens van 78 leerlingen. Hoeveel studenten zou je verwachten in het BSO bij basisschool A als er statistische onafhankelijkheid zou zijn tussen school en stroom?

School	ASO	BSO	TSO	KSO	Totaal
Basisschool A	7	8	13	5	33
Basisschool B	17	12	11	5	45
Totaal	24	20	24	10	78

• gegeven
  • $X$: basisschool
  • $Y$: stroom
  • $n = 78$
• gevraagd
  • $E_{BSO, A}$ indien $X, Y$ onafhankelijk
• oplossing
  • $E_{BSO, A} = \dfrac{20 \cdot 33}{78} \approx 8.4615$

Bereken de toetsstatistiekwaarde om na te gaan of er een samenhang is tussen basisschool en stroom.

School	ASO	BSO	TSO	KSO	Totaal
Basisschool A	10.1538	8.4615	10.1538	4.2308	33
Basisschool B	13.8462	11.5385	13.8462	5.7692	45
Totaal	24	20	24	10	78

• gevraagd
  • $ts$
• oplossing
  • $TS = X^2 = \sum_{i=1}^I \dfrac{(O_i - E_i)^2}{E_i} \sim \chi^2_{df=I-1-k}$ onder $H_0$
  • $ts \approx 3.3669$ (ZRM)
  • $df = 3 \cdot 1 = 3$

Wat is de kritieke waarde voor een $\chi^2$−toets om de samenhang tussen variabele $X$ met 3 niveaus en variabele $Y$ met 4 niveaus na te gaan zonder verdere modelveronderstellingen ($\alpha = 0.01$)?

• gegeven
  • $m = 3$
  • $m' = 4$
  • $\alpha = 0.01$
• gevraagd
  • kritieke $\chi^2$ waarde
• oplossing
  • $df = (3-1)(4-1) = 6$
  • eenzijdige alternatieve hypothese (rechterstaart verdacht)
    • dus we moeten $\alpha$ niet meer door twee delen
  • $x^{2*}_{0.99} = 16.8119$

10.3 Algemeen model

• waardebereik opdelen in $I$ niet-overlappende en niet-lege categorieen

Een psycholoog onderzoekt de reactietijden van proefpersonen bij het oplossen van een eenvoudige taak. Volgens eerder onderzoek zouden de reactietijden normaal verdeeld moeten zijn met een gemiddelde van 500 ms en een standaardafwijking van 100 ms. De psycholoog meet de reactietijden van 120 personen (samengevat in onderstaande tabel). Toets of het model de geobserveerde gegevens fit.

Reactietijden	$O_i$	$E_i$
$< 400$	25
$400 - 500$	50
$500 - 600$	35
$> 600$	10

• gegeven
  • $X$: reactietijd (ms)
  • $n = 120$
• gevraagd
  • $X \sim N(500, 100^2)$?
• oplossing
  • $P(X < 400) = P(Z < -1) \approx 0.160$
  • $P(400 < X < 500) = P(-1 < Z < 0) = P(Z < 0) - P(Z < -1) \approx 0.500 - 0.160 = 0.340$
  • $P(500 < X < 600) = P(0 < Z < 1) \approx 0.340$ (symmetrie)
  • $P(X > 600) = P(Z > 1) \approx 0.160$ (symmetrie)

Reactietijden	$O_i$	$E_i$
$< 400$	$25$	$120 \cdot 0.160 = 19.2$
$400 - 500$	$50$	$120 \cdot 0.340 = 40.8$
$500 - 600$	$35$	$120 \cdot 0.340 = 40.8$
$> 600$	$10$	$120 \cdot 0.160 = 19.2$

• oplossing (vervolg)
  • check voorwaarden
    • ✅ $\forall i: E_i > 5$
  • stap 1
    • $H_0: X \sim N(500, 100^2)$
    • $H_1: X \not\sim N(500, 100^2)$
  • stap 2
    • $n = 120$
    • $\alpha = ?$
  • stap 3
    • $TS = X^2 = \sum_{i=1}^I \dfrac{(O_i - E_i)^2}{E_i} \sim \chi^2_{df=I-1-k}$ onder $H_0$
      • $k = 0$ ($\mu_X$ en $\sigma_X^2$ zijn gegeven en werden niet geschat uit de observaties)
      • $df = 4 - 1 - 0 = 3$
  • stap 4
    • $ts \approx 1.7521 + 2.0745 + 0.8245 + 4.4083 \approx 9.0594$
  • stap 5
    • rechterstaart verdacht
  • stap 6
    • $p = P(X^2 > 9.0594) = 1-P(X^2 \leq 9.0594)$
    • $0.025 < p < 0.030$
    • conclusie
      • hangt af van $\alpha$
      • verwerp $H_0$ voor $\alpha = 0.05$
      • dus $X$ niet normaal verdeeld